Veamos algunos conceptos previos :
a) Conjunto de los números reales
Está formado por el conjunto de los números enteros, racionales e irracionales, en adelante lo vamos a denotar por R ; gráficamente el conjunto de los números reales lo podemos representar por una recta en la que fijamos un origen y una unidad, que hace que a cada punto de la recta le corresponda un número real y a cada número real le corresponda un punto de la recta. A esta recta la denominamos la recta realb)Función : Dados dos conjuntos A y B, llamamos función a la correspondencia de A en B en la cual todos los elementos de A tienen a lo sumo una imagen en B, es decir una imagen o ninguna.
Es una relación entre los elementos de dos conjuntos, de forma que a determinados elementos del primer conjunto se asocian elementos del segundo conjunto de manera unívoca, es decir que a un elemento del primer conjunto no le podemos asociar más de un elemento del segundo conjunto. A un elemento cualquiera del primer conjunto lo representamos con la letra x, que denominamos variable independiente y al único elemento que le corresponde en el segundo conjunto lo representamos por la letra y, a la que denominamos variable dependiente. A la relación la representamos por la letra f y escribimos y=f(x).c)Dominio de definición de una función f :
Es el conjunto de valores de x para los que la función f(x) existe. Lo representamos pord)Recorrido o imagen de una función f :
Es el conjunto de valores que toma la variable dependiente y. Lo representamos porEs aquella cuyo dominio y recorrido son subconjuntos del conjunto de los números reales.
Función real de variable real
Las funciones reales de variable real se suelen representar en el plano, utilizando un sistema de referencia.(video) En la figura que sigue, la primera gráfica, es la gráfica de una función ; la segunda, no es la gráfica de una función:
Una función puede definirse mediante una expresión verbal, una tabla, una fórmula o una gráfica. En general trabajaremos con funciones expresadas mediante una fórmula o expresión analítica y su gráfica. Según la expresión analítica clasificamos las funciones de la siguiente forma:
Intervalos y entornos (Video)
Definimos sobre la recta real :El conjunto [a,b] se llama intervalo cerrado y (a,b) se llama intervalo abierto. En cualquiera de los casos b-a se llama longitud del intervalo.
Entorno de un número real x: (video)
Si X es un espacio topológico y p es un punto perteneciente a X, un entorno de p es un conjunto V que contiene un conjunto abierto U que contiene a p,
Nótese que el entorno V no necesita ser un conjunto abierto. Si V es abierto se lo llama un entorno abierto. Algunos autores especifican que los entornos deben ser abiertos, por lo que es importante prestar cuidado a las diferentes notaciones.
El conjunto de todos los entornos de un punto forma una base de entornos del punto.
Si S es un subconjunto de X, un entorno de S es un conjunto V, que contiene un conjunto abierto U que contiene a S. Se deduce que un conjunto V es un entorno de S si y solo si es un entorno de todos los puntos de S.

En análisis real para funciones de una variable, se puede hacer una definiciónde límite similar a la de límite de una sucesión, en la cual, los valores que toma la función dentro de un intervalo o radio de convergencia se van aproximando a un punto fijado c, independientemente de que éste pertenezca al dominio de la función. El punto c es punto de acumulación del dominio de la función.1 Esto se puede generalizar aún más a funciones de varias variables o funciones en distintos espacios métricos.
Informalmente, se dice que el límite de la función f(x) es L cuando x tiende a c, y se escribe:
si se puede encontrar para cada ocasión un x suficientemente cerca de c tal que el valor de f(x) sea tan próximo a L como se desee.
Para un mayor rigor matemático se utiliza la definición épsilon-delta de límite, que es más estricta y convierte al límite en una gran herramienta del análisis real. Su definición es la siguiente:
"El límite de f(x) cuando x tiende a c es igual a L si y sólo si para todo número real ε mayor que cero existe un número real δ mayor que cero tal que si la distancia entre x y c es menor que δ, entonces la distancia entre laimagen de x y L es menor que ε unidades".
Esta definición, se puede escribir utilizando términos lógico-matemáticos y de manera compacta:






























"La existencia del limite de una funcion f(x), esta condicionado por la existencia de los limites laterales de f(x)"
Límites laterales (video)
respectivamente. Si los dos límites anteriores son iguales a L entonces estos se pueden referir como el límite de f(x) en c.
Dicho de otro modo, si los limites laterales no son iguales a L entonces el límite, como tal, no existe.
Cálculo del límite de una función en un punto
Si f(x) es una función usual (polinómicas, racionales, radicales, exponenciales, logarítmicas, etc.) y está definida en el punto a, entonces se suele cumplir que:

Es decir: para calcular el límite se sustituye en la función el valor al que tienden las x.



No podemos calcular  porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.
porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.
 porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.
porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.
Sin embargo si podemos calcular  , aunque 3 no pertenezca al dominio, D=
, aunque 3 no pertenezca al dominio, D=  − {2, 3}, si podemos tomar valores del dominio tan próximos a 3 como queramos.
− {2, 3}, si podemos tomar valores del dominio tan próximos a 3 como queramos.
 , aunque 3 no pertenezca al dominio, D=
, aunque 3 no pertenezca al dominio, D=  − {2, 3}, si podemos tomar valores del dominio tan próximos a 3 como queramos.
− {2, 3}, si podemos tomar valores del dominio tan próximos a 3 como queramos.Cálculo del límite de una función definida por trozos
En primer lugar tenemos que estudiar los límites laterales en los puntos de unión de los diferentes trozos.
Si coinciden, este es el valor del límite.
Si no coinciden, el límite no existe.
 .
.
En x = −1, los límites laterales son:
Por la izquierda:

Por la derecha:

Como en ambos casos coinciden, existe el límite y vale 1.
En x = 1, los límites laterales son:
Por la izquierda:

Por la derecha:

Como no coinciden los límites laterales no tiene límite en x = 1.




































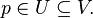

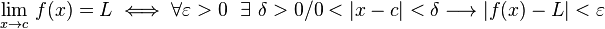

 o
o 





