Interpretación geométrica y cociente de diferencias de Newton
La derivada de una función
 es la pendiente geométrica de la línea tangente del gráfico de
es la pendiente geométrica de la línea tangente del gráfico de  en
en  . Sin el concepto que se va a definir, no es posible encontrar directamente la pendiente de la línea tangente a una función dada, porque solamente se conoce un punto en la línea tangente:
. Sin el concepto que se va a definir, no es posible encontrar directamente la pendiente de la línea tangente a una función dada, porque solamente se conoce un punto en la línea tangente: 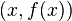 . La idea es aproximar la línea tangente con múltiples líneas secantes que tienen distancias progresivamente más pequeñas entre los dos puntos que cruzan. Cuando se toma el límite de las pendientes de las líneas secantes de esta progresión, se consigue la pendiente de la línea tangente. Se define, pues, la derivada tomando el límite de la pendiente de las líneas secantes, al acercarlas a la línea tangente.
. La idea es aproximar la línea tangente con múltiples líneas secantes que tienen distancias progresivamente más pequeñas entre los dos puntos que cruzan. Cuando se toma el límite de las pendientes de las líneas secantes de esta progresión, se consigue la pendiente de la línea tangente. Se define, pues, la derivada tomando el límite de la pendiente de las líneas secantes, al acercarlas a la línea tangente.Para encontrar las pendientes de las líneas secantes próximas, se elige un número
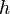 relativamente pequeño.
relativamente pequeño. 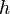 representa un cambio relativamente pequeño en
representa un cambio relativamente pequeño en  , el cual puede ser positivo o negativo. La pendiente de la línea que cruza los dos puntos
, el cual puede ser positivo o negativo. La pendiente de la línea que cruza los dos puntos 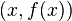 y
y  es
es
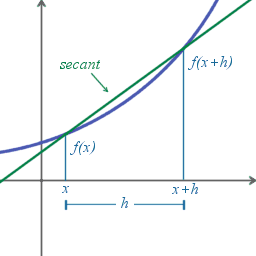
Esta expresión es el cociente de diferencias de Newton. La derivada de f en x es el límite del valor del cociente diferencial, conforme las líneas secantes se aproximan a la línea tangente: .
. existe en todos los puntos
existe en todos los puntos  , se puede definir la derivada de
, se puede definir la derivada de  como la función cuyo valor en cada punto
como la función cuyo valor en cada punto  es la derivada de
es la derivada de  en
en  .
.Puesto que sustituir
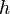 por 0 produce una división por cero, calcular directamente la derivada puede no ser intuitivo. Una técnica posible consiste en operar en el numerador, de manera que se pueda cancelar la
por 0 produce una división por cero, calcular directamente la derivada puede no ser intuitivo. Una técnica posible consiste en operar en el numerador, de manera que se pueda cancelar la 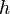 del denominador. Y eso es posible fácilmente en los polinomios. Pero para muchas otras funciones el resultado es incierto. Afortunadamente, hay reglas generales que facilitan diferenciar la mayoría de las funciones simples.
del denominador. Y eso es posible fácilmente en los polinomios. Pero para muchas otras funciones el resultado es incierto. Afortunadamente, hay reglas generales que facilitan diferenciar la mayoría de las funciones simples.Sea
 una función continua, y
una función continua, y  su curva. Sea
su curva. Sea  la abscisa de un punto regular, es decir donde
la abscisa de un punto regular, es decir donde  no hace un ángulo. En el punto
no hace un ángulo. En el punto  de
de  se puede trazar la tangente a la curva. Su coeficiente director, o sea su pendiente, es
se puede trazar la tangente a la curva. Su coeficiente director, o sea su pendiente, es  , el número derivado de
, el número derivado de  en
en  .
.La función
 es la derivada de
es la derivada de  .
.
 , se puede saber a qué ritmo crece o decrece la función. El signo de
, se puede saber a qué ritmo crece o decrece la función. El signo de  determina si la función
determina si la función  crece o decrece.
crece o decrece. Veamos una explicacion un poco mas entretenida:
Ejemplo de aplicacion del concepto geométrico de la derivada de una función
Hallar la derivada de la función f(x) = 3x2 en el punto x = 2.


BIEN VAMOS A RECREO.......
No hay comentarios:
Publicar un comentario